Collecting Verification Codes (1)

• Introduction
• Problem Statement
• Solution
  • Solution 1
  • Solution 2
• Conclusion

Introduction

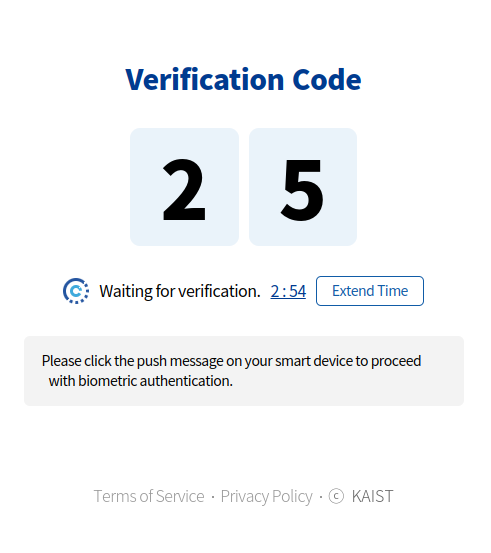
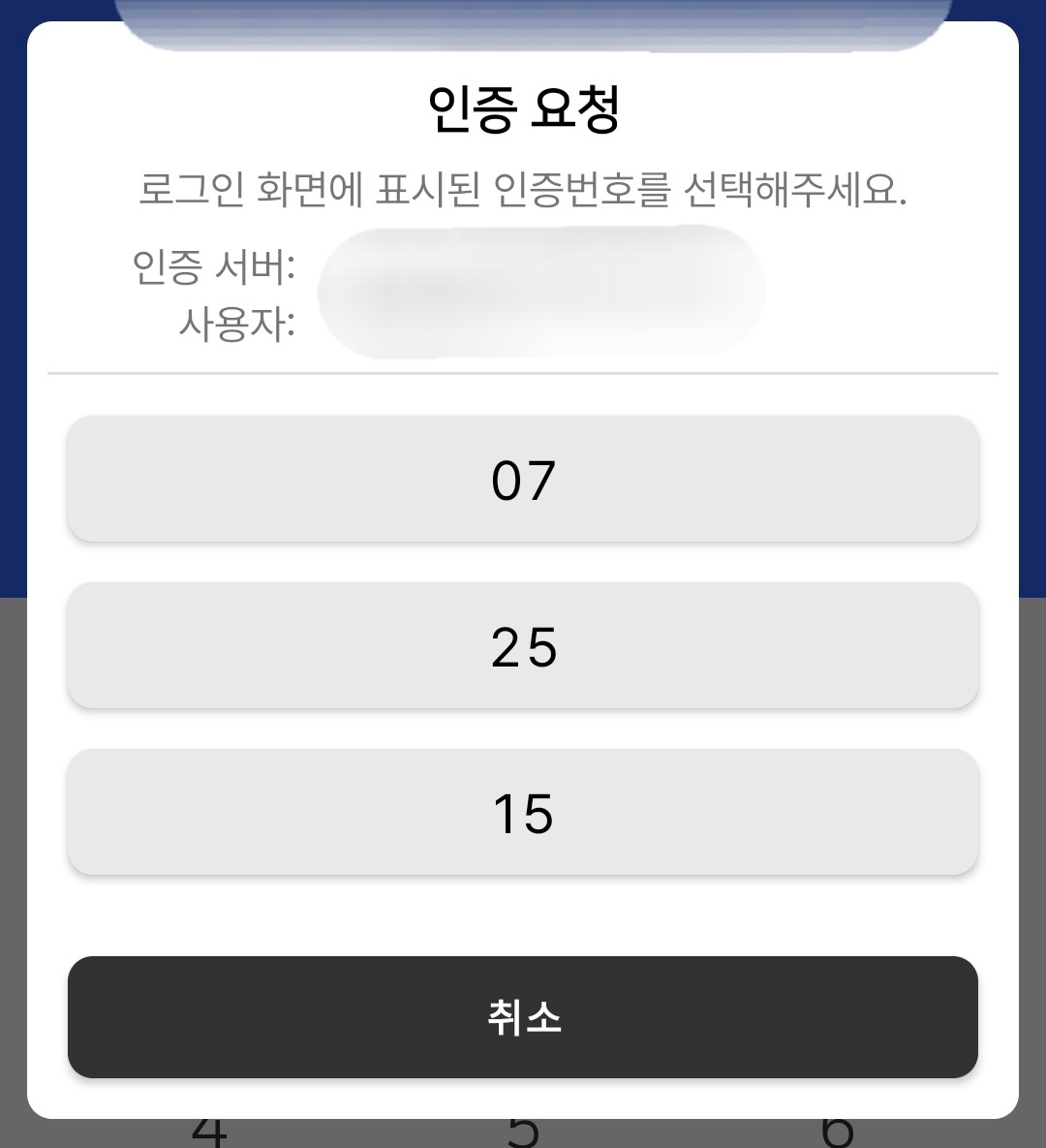
When I try to log into my university’s SSO system, it gives me a two-digit verification code that I must select on my cellphone. For instance, in the images below, the website (on the left) shows the number 25, and I would tap 25 on my phone (on the right). Now, I’m curious about how many attempts I would need to make to see all possible 100 codes.

Problem Statement

Let \(S\) be a finite set of size \(N\). At the beginning, a set \(F\) is initialized to be an empty set. For each step, a random element \(r\) is chosen at uniformly random from \(S\) and put to \(F\), i.e., \(F \leftarrow F \cup \{ r \}\). Then, what is the expected number of steps to reach \(S = F\)?

Now, take your time to solve this problem! (Hint: it is easy.)

Solution

Solution 1

For fixed \(N\), suppose there are \(n\) elements should be chosen to reach \(S = F\). In other words, \(n = |S \setminus F|\). Now, let \(a_n\) be the expected number of additional steps at the moment. We let \(a_0 = 0\).

Then, we have \(n/N\) probability of getting a new fresh number and \(1-n/N\) probability of getting a number that has been chosen before. Thus, noticing that we need this one step to choose an element, we have the following recursive formula:

\begin{equation} a_n = 1 + \frac{n}{N} \cdot a_{n-1} + \left(1 - \frac{n}{N}\right) \cdot a_n \end{equation}

Rearranging, we get

\begin{equation}\label{eq:2} a_n = a_{n-1} + \frac{N}{n}\text{.} \end{equation}

Equation \eqref{eq:2} directly gives

\begin{equation} a_n = N \cdot \sum_{i=1}^n \frac{1}{i} = N \cdot H_n \end{equation}

where \(H_n\) is the \(n\)-th harmonic number.

In particular, we have \(a_N = N \cdot H_N\). (In fact, this solution needs more verification that each \(a_i\) exists but I omit.)

Solution 2

For fixed \(N\), let \(X_i\) be a random variable for the number of steps until the next element which has not been chosen before when there are \(i\) elements not chosen. Then, we immediately get \(\mathbb{E}[X_i] = N/i\). Then, \(X\), the random variable for the number of steps to reach \(F = S\) equals \(\sum_{i=1}^N X_i\); by linearity, we get

\[\mathbb{E}[X] = \sum_{i=1}^N \mathbb{E}[X_i] = N \cdot \sum_{i=1}^N \frac{1}{i} = N \cdot H_N\text{.}\]

Conclusion

Hence, as \(100 \cdot H_{100} \approx 518.74\), I shall expect about 519 log-in tries to observe all 100 numbers.